C++11以降において,立方根(三乗根)の計算の際に,一般的に数学関数(<cmath>ヘッダ)を使用します.

平方根関数std::sqrtはよく知られていますが,
立方根std::cbrtは意外と知られていません
立方根の算出するべき乗関数std::pow(x,1/3)と立方根関数std::cbrtの速度比較をしました.



std::cbrtとstd::powどちらを使うべき?



結論は…std::cbrtが高速です
>> Optimized C++ ―最適化、高速化のためのプログラミングテクニック
目次
検証



↓↓↓検証結果はこちら↓↓↓
結果
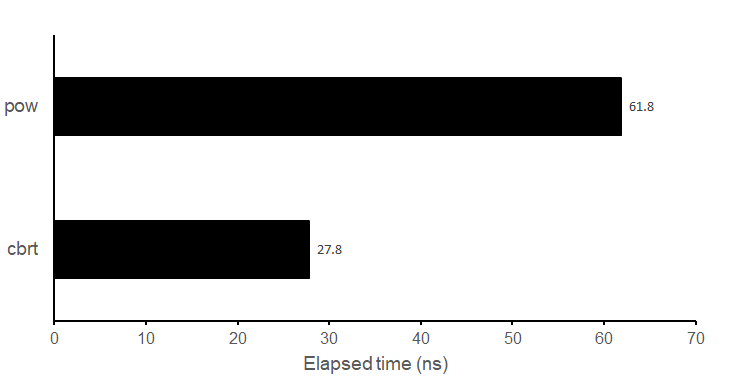
最適化なし(-O0)
std::cbrtはstd::powの約2倍高速な結果となりました.

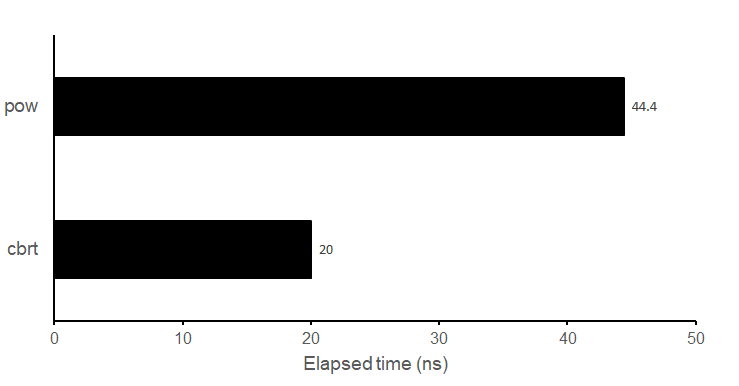
最適化あり(-O2)
最適化を行った場合,std::cbrtはstd::powの約2倍高速な結果となりました.

検証に使用したコード
速度検証のため,Google Benchmarkを使用しました.
Google Benchmarkに関しては別記事にしています.下記記事をご覧ください.
あわせて読みたい




C++でのベンチマークテストのためにGoogle Benchmarkライブラリを利用する
便利なベンチマークツールは使うべし! 単体テストは重要性は近年では広く周知されています.一方で,性能に関してはなかなか議論されることが多くありません. その一…
検証に使用したコードは下記のようになります.
#include <benchmark/benchmark.h>
#include <cmath>
#include <iostream>
#include <random>
static void plus(benchmark::State& state)
{
std::random_device seed;
std::mt19937 rng(seed());
std::uniform_real_distribution<> distr(-M_PI_2, M_PI_2);
double sum = 0.0e0;
for (auto _ : state)
{
sum += distr(rng);
}
// prevent ignore code by optimization
std::cout << sum << std::endl;
}
BENCHMARK(plus);
static void cbrt(benchmark::State& state)
{
std::random_device seed;
std::mt19937 rng(seed());
std::uniform_real_distribution<> distr(0.0e0, 1000.0e0);
double sum = 0.0e0;
for (auto _ : state)
{
sum += std::cbrt(distr(rng));
}
// prevent ignore code by optimization
std::cout << sum << std::endl;
}
BENCHMARK(cbrt);
static void pow_cbrt(benchmark::State& state)
{
std::random_device seed;
std::mt19937 rng(seed());
std::uniform_real_distribution<> distr(0.0e0, 1000.0e0);
double sum = 0.0e0;
for (auto _ : state)
{
sum += std::pow(distr(rng), 1.0e0 / 3.0e0);
}
// prevent ignore code by optimization
std::cout << sum << std::endl;
}
BENCHMARK(pow_cbrt);
BENCHMARK_MAIN();
検証結果において乱数生成と加算の計算時間は,別途減算しています.
結論
std::cbrtとstd::powの立方根算出速度には有意な差がありました.
その一方で,以前に平方根の算出速度も比較したstd::sqrtとstd::powほどの差はありませんでした.
その理由は,平方根の算出アルゴリズムと立方根アルゴリズムが異なり,立方根アルゴリズムの計算負荷が大きいためでしょう.
↓↓↓以前に比較した平方根の算出速度はこちらの記事に↓↓↓


