【Python】 データ補完はScipyによる内挿が便利

離散データに対して補完を行いたい場合，なんらかの関数近似を用いることが一般的です．

PythonではScipyライブラリ（scipy.interpolate）にいくつかの近似関数が用意されており，それらを使用することで簡単にデータ補完（内挿）を行うことができます．

スプラインなどの有名どころの補完は用意されているのは大きなメリットです．

ここでは，下記の補完方法に対して実装します．

• 線形補完
• 2次補完
• 3次補完
• 区分的3次エルミート補完（PCHIP）
• 最近傍補完
• Barycentric補完
• Krogh補完
• Akima補完

Scipyで用意されている内挿一覧はこちらにあります．

各補完方法による比較は後述していますが，CubicやPCHIPが比較的多くの場面で使用されます．

対象の関数

補完する関数として以下の３パターンを対象とします．

• Sin関数
• Sin関数（ノイズ10%）
• ヘビサイド関数

Sin関数

Sin関数（ノイズ10%）

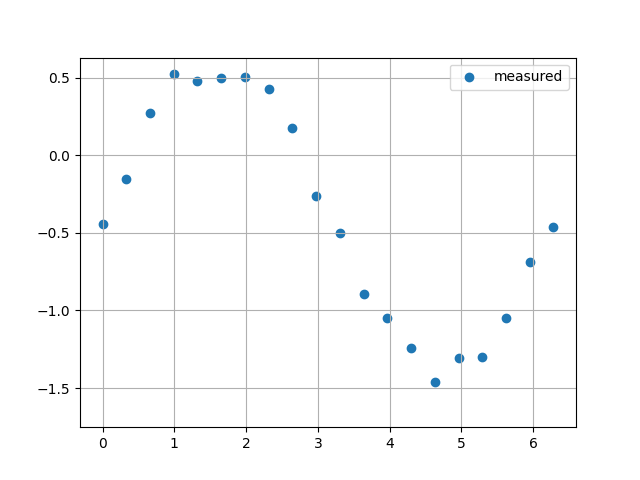
ヘビサイド関数

Scipyによる補完結果

線形補完

Sin関数

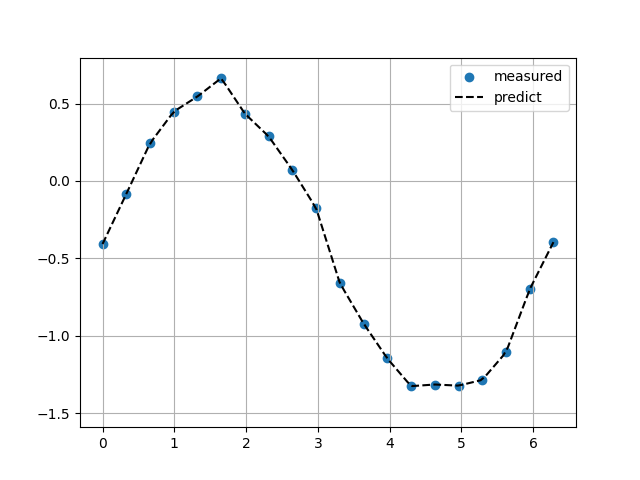
Sin関数（ノイズ10%）

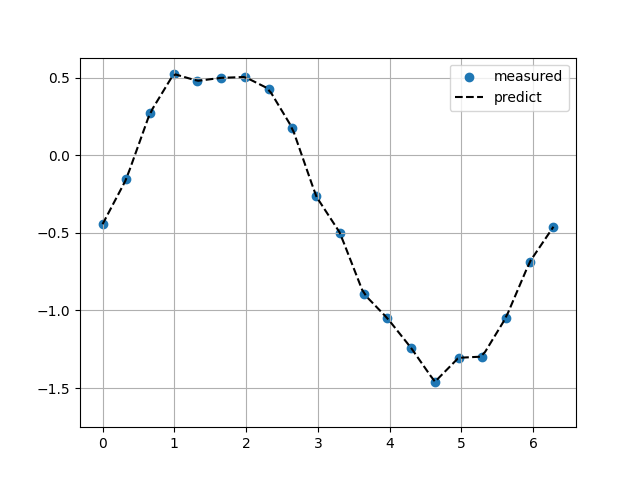
ヘビサイド関数

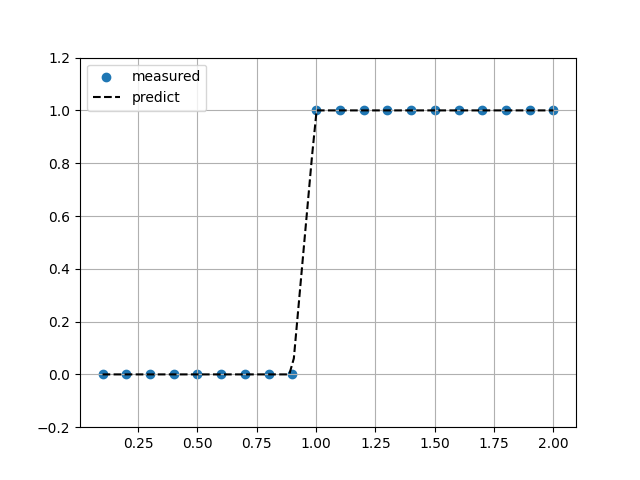
2次補完

Sin関数

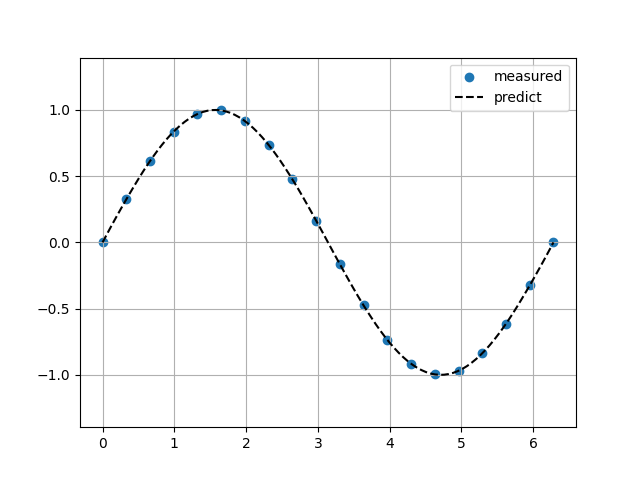
Sin関数（ノイズ10%）

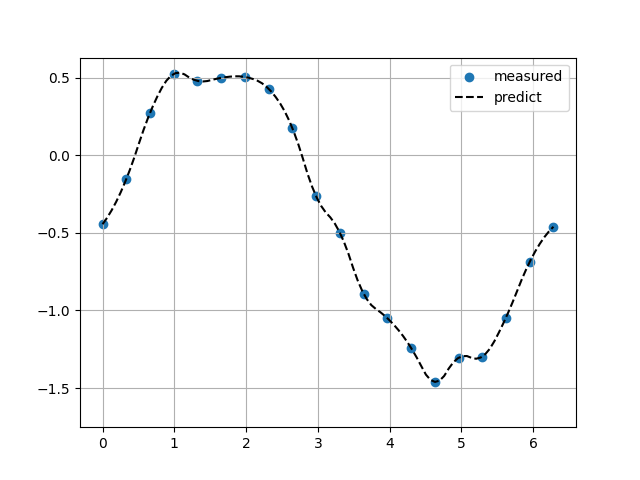
ヘビサイド関数

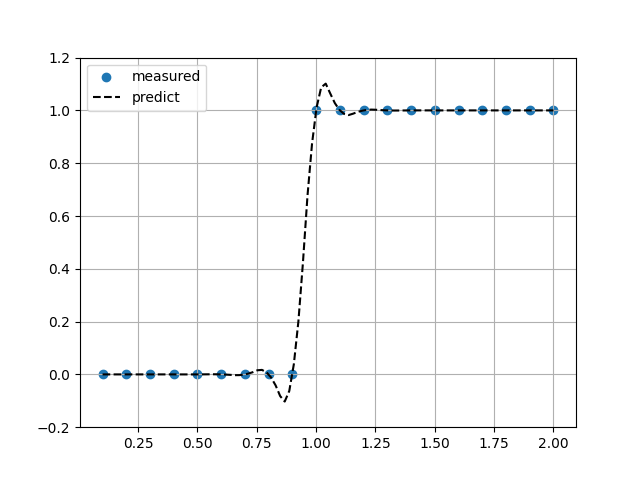
3次補完

Sin関数

Sin関数（ノイズ10%）

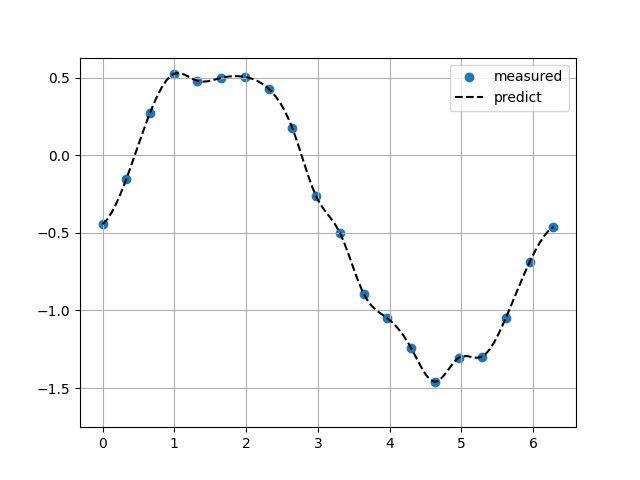
ヘビサイド関数

区分的3次エルミート補完（PCHIP）

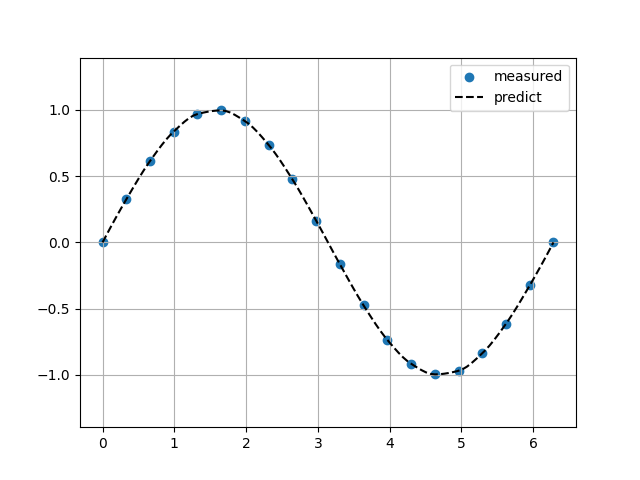
Sin関数

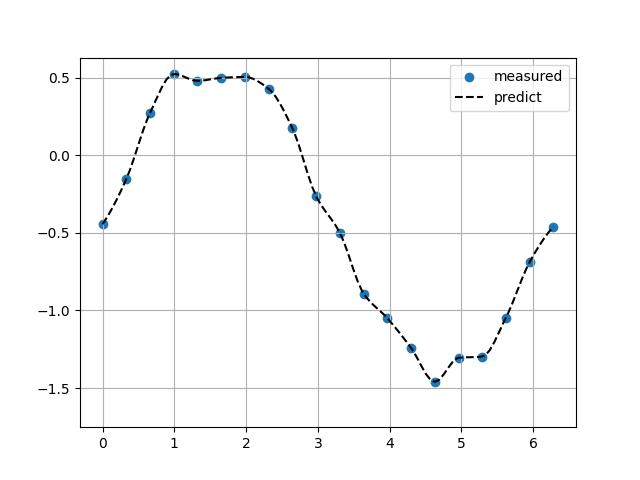
Sin関数（ノイズ10%）

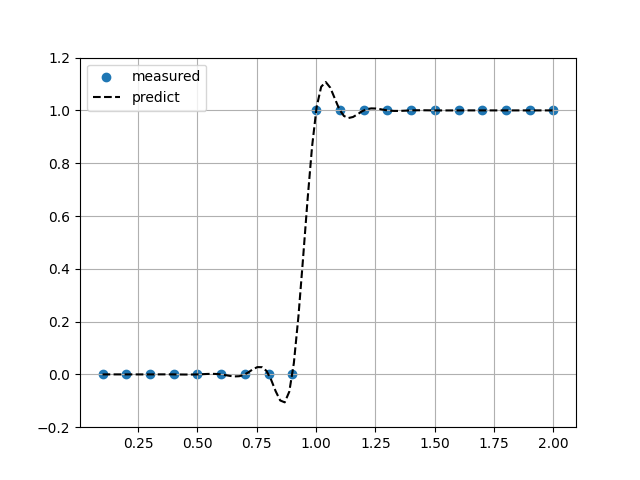
ヘビサイド関数

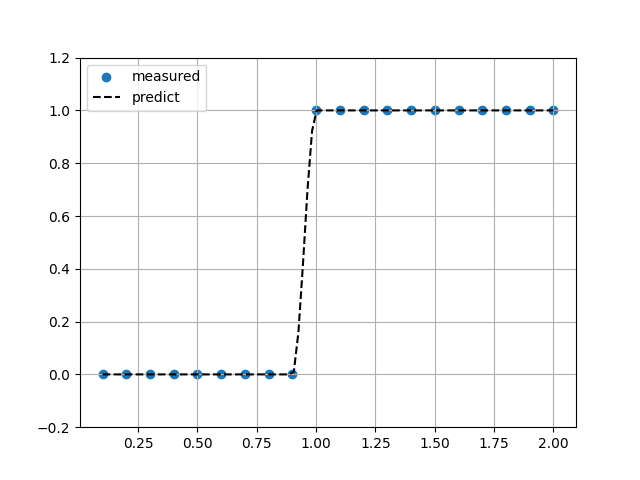
最近傍補完

Sin関数

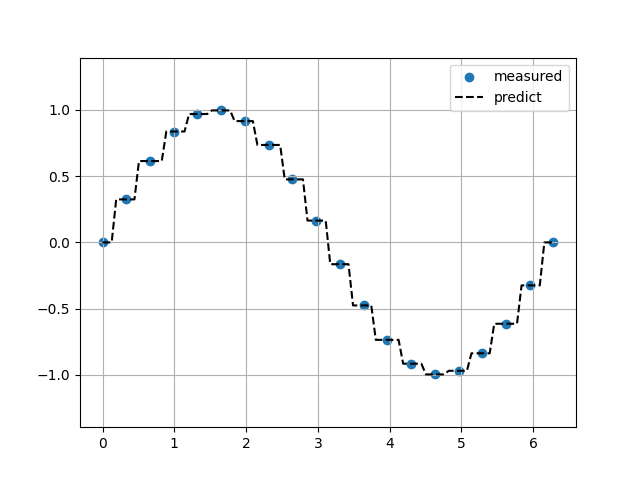
Sin関数（ノイズ10%）

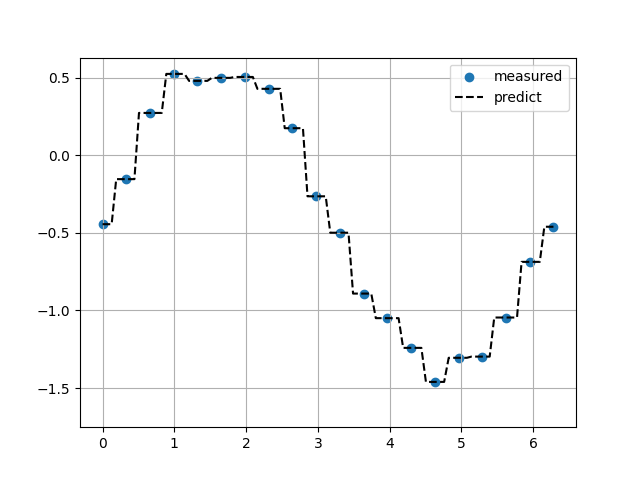
ヘビサイド関数

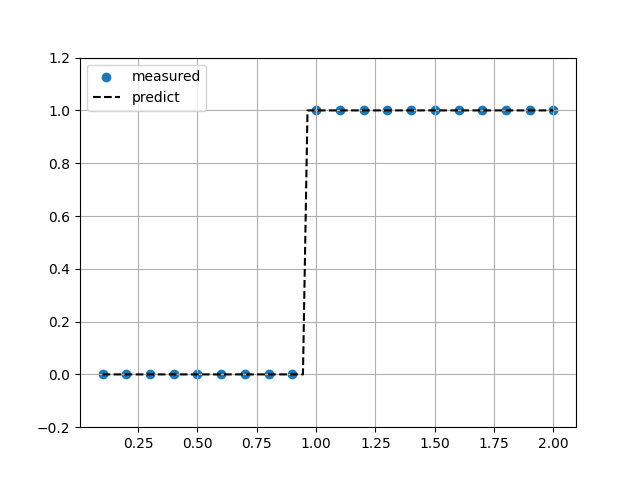
Barycentric補完

Sin関数

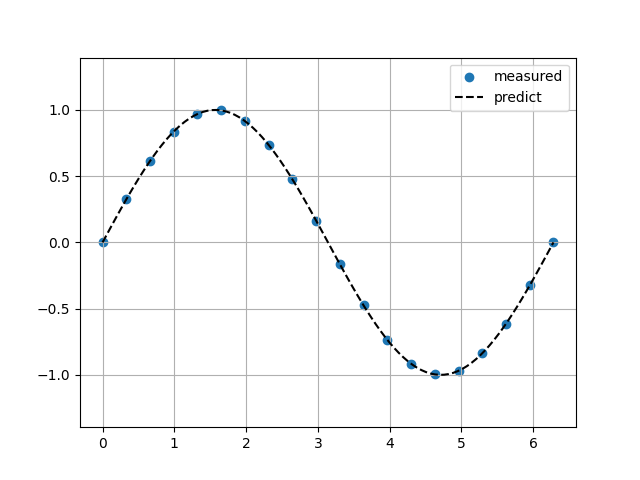
Sin関数（ノイズ10%）

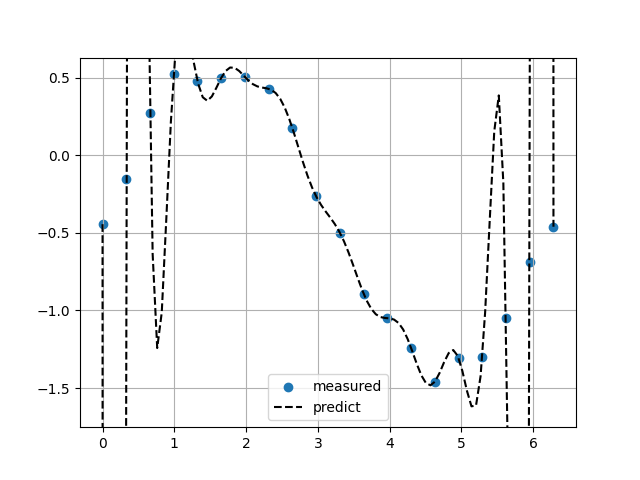
ヘビサイド関数

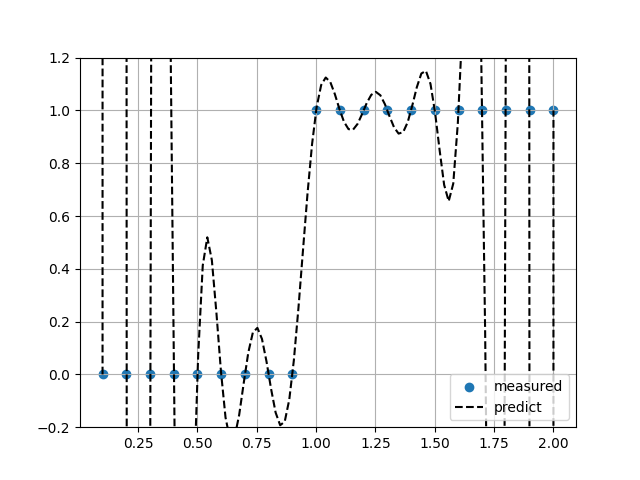
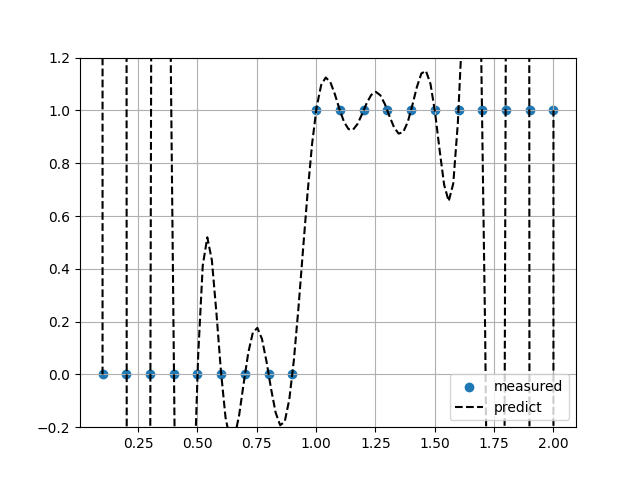
Krogh補完

Sin関数

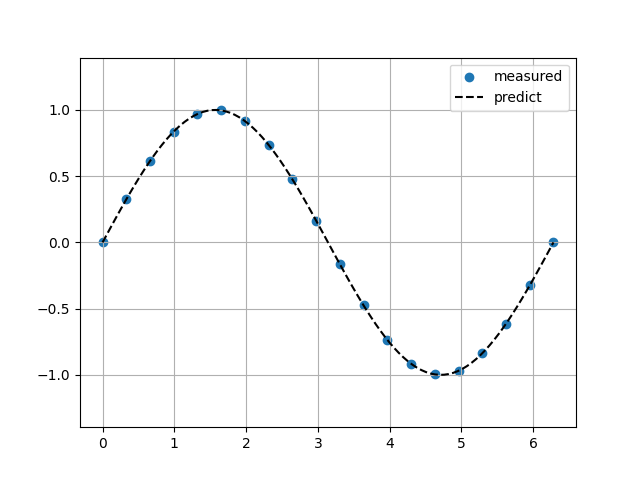
Sin関数（ノイズ10%）

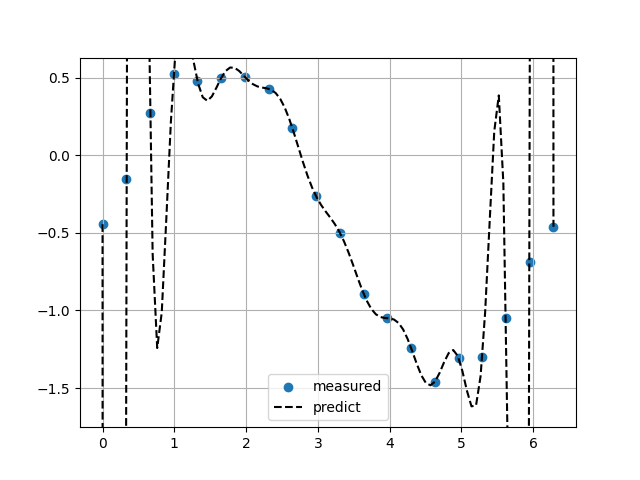
ヘビサイド関数

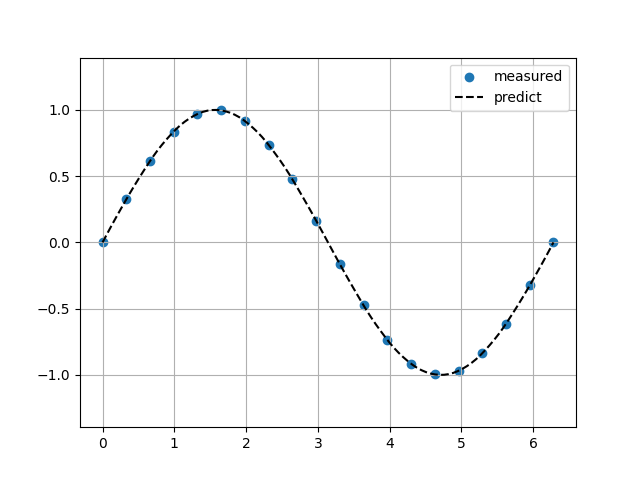
Akima補完

Sin関数

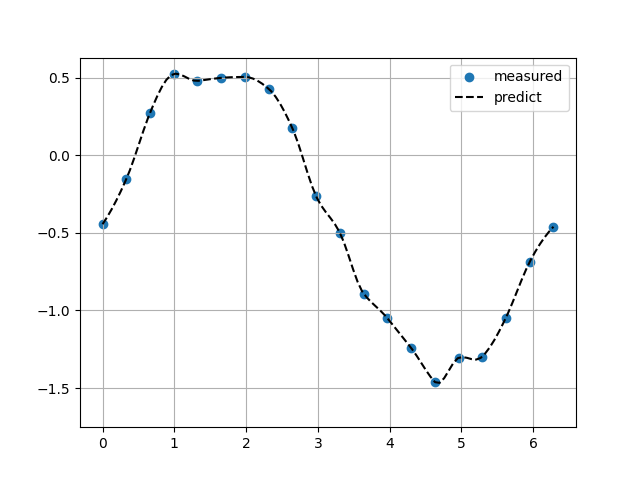
Sin関数（ノイズ10%）

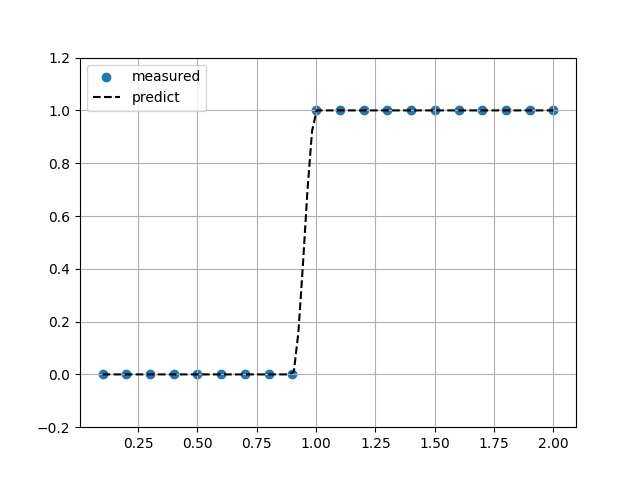
ヘビサイド関数

使用したコード

from cmath import pi
import numpy as np
from io import TextIOWrapper
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate


def create_scatter_data() -> np.ndarray:
    x = np.linspace(0, 2 * pi, 20)
    y = np.sin(x)
    return np.stack((x, y), axis=1)


def main():
    data = create_scatter_data()
    list = [
        ["Linear", lambda x, y: interpolate.interp1d(x, y, kind="linear")],
        ["Quadratic", lambda x, y: interpolate.interp1d(x, y, kind="quadratic")],
        ["Cubic", lambda x, y: interpolate.interp1d(x, y, kind="cubic")],
        ["Nearest", lambda x, y: interpolate.interp1d(x, y, kind="nearest")],
        ["PCHIP", interpolate.PchipInterpolator],
        ["Barycentric", interpolate.BarycentricInterpolator],
        ["Krogh", interpolate.KroghInterpolator],
        ["Akima", interpolate.Akima1DInterpolator],
    ]
    x = np.linspace(min(data[:, 0]), max(data[:, 0]), 100)
    for name, interpolation in list:
        y = interpolation(data[:, 0], data[:, 1])
        plt.scatter(data[:, 0], data[:, 1], label="measured")
        plt.plot(x, y(x), label="predict", color="black")
        yl = max(data[:, 1]) - min(data[:, 1])
        plt.ylim(min(data[:, 1]) - yl * 0.2, max(data[:, 1]) + yl * 0.2)
        plt.grid()
        plt.legend()
        plt.savefig(name+".png")
        plt.clf()


if __name__ == "__main__":
    main()